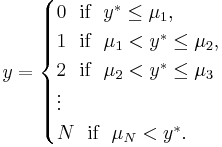Ordered logit

In statistics, the ordered logit model (also ordered logistic regression or proportional odds model), is a regression model for ordinal dependent variables. It can be thought of as an extension of the logistic regression model for dichotomous dependent variables, allowing for more than two (ordered) response categories.

The model only applies to data that meet the proportional odds assumption, that the relationship between any two pairs of outcome groups is statistically the same. This means that

the coefficients that describe the relationship between, say, the lowest versus all higher categories of the response variable are the same as those that describe the relationship between the next lowest category and all higher categories, etc....Because the relationship between all pairs of groups is the same, there is only one set of coefficients.[1]

The model cannot be consistently estimated using ordinary least squares; it is usually estimated using maximum likelihood.

Examples of multiple ordered response categories include bond ratings, opinion surveys with responses ranging from "strongly agree" to "strongly disagree," levels of state spending on government programs (high, medium, or low), the level of insurance coverage chosen (none, partial, or full), and employment status (not employed, employed part time, or fully employed).[2]

Suppose the underlying process to be characterized is

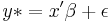y* =x' \beta %2B \epsilon,

where y* is the exact but unobserved dependent variable (perhaps the exact level of agreement with the statement proposed by the pollster); x is the vector of independent variables, and \beta is the vector of regression coefficients which we wish to estimate. Further suppose that while we cannot observe y*, we instead can only observe the categories of response

y= \begin{cases} 0~~ \text{if}~~y^* \le \mu_1, \\ 1~~ \text{if}~~\mu_1<y^* \le \mu_2, \\ 2~~ \text{if}~~\mu_2 <y^* \le \mu_3 \\ \vdots \\ N~~ \text{if}~~ \mu_{N} < y^*. \end{cases}

Then the ordered logit technique will use the observations on y, which are a form of censored data on y*, to fit the parameter vector \beta.

See also

References

  1. ^ http://www.ats.ucla.edu/stat/r/dae/ologit.htm
  2. ^ Greene, William H., Econometric Analysis (fifth edition), Prentice Hall, 2003, 736-740.

Further reading